Complete the derivation of the invariance of the interval given in Box 2.4, using the Principle of Relativity in the form that the laws of physics must be the same in theprimed and unprimed frames. (a) Having carried out the construction in the unprimed frame, depicted at the bottom left of Box 2.4, use the same mirror and photons for the analogous construction in the primed frame. Argue that, independently of the frame in which the mirror is at rest (unprimed or primed), the fact that the reflected photon has (angle of reflection) = (angle of incidence) in its rest frame implies that this is also true for the same photon in the other frame. Thereby conclude that the construction leads to Eq. (1b) in Box 2.4, as well as to Eq. (1a).

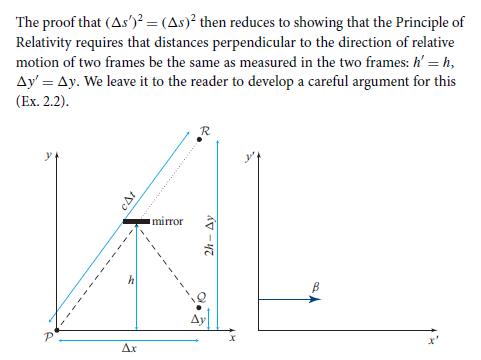
(b) Then argue that the perpendicular distance of an event from the common x- and x´-axes must be the same in the two reference frames, so h´ = h and △y´= △y; whence Eqs. (1b) and (1a) in Box 2.4 imply the invariance of the interval.

Transcribed Image Text:

BOX 2.4. PROOF OF INVARIANCE OF THE INTERVAL FOR A TIMELIKE SEPARATION A simple demonstration that the interval is invariant is provided by a thought experiment in which a photon is emitted at event P, reflects off a mirror, and is then detected at event Q. We consider the interval between these events in two reference frames, primed and unprimed, that move with respect to each other. Choose the spatial coordinate systems of the two frames in such a way that (i) their relative motion (with speed ß, which will not enter into our analysis) is along the x and x' directions, (ii) event P lies on the x and x' axes, and (iii) event Q lies in the x-y and x'-y' planes, as depicted below. Then evaluate the interval between P and Q in the unprimed frame by the following construction: Place the mirror parallel to the x-z plane at precisely the heighth that permits a photon, emitted from P, to travel along the dashed line to the mirror, then reflect off the mirror and continue along the dashed path, arriving at event Q. If the mirror were placed lower, the photon would arrive at the spatial location of Q sooner than the time of Q; if placed higher, it would arrive later. Then the distance the photon travels (the length of the two-segment dashed line) is equal to cAt = At, where At is the time between events P and Q as measured in the unprimed frame. If the mirror had not been present, the photon would have arrived at event R. after time At, so cAt is the distance between P and R. From the diagram, it is easy to see that the height of R above the x-axis is 2h - Ay, and the Pythagorean theorem then implies that (As)² = -(At)² + (Ax)² + (Ay)² = -(2h - Ay)² + (Ay)². (1a) The same construction in the primed frame must give the same formula, but with primes: (As)² = -(At)² + (Ax)² + (Ay)² = -(2h' - Ay)² + (Ay)². (1b)