Consider a collection of thermalized, classical particles with nonzero rest mass, so they have the Boltzmann distribution. Assume that the temperature is low enough (k_BT ≪ mc²) that they are nonrelativistic.(a) Explain why the total number density of particles n in physical space (as measured in the particles’ mean rest frame) is given by the integral

Show that n ∝ e^μ/^k_BT, and derive the proportionality constant.

(b) Explain why the mean energy per particle is given by

Show that E̅ = 3/2k_BT.

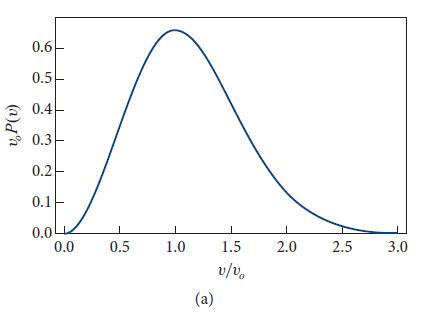
(c) Show that P(v)dv ≡ (probability that a randomly chosen particle will have speed v ≡ |v| in the range dv) is given by

This is called the Maxwell velocity distribution; it is graphed in Fig. 3.6a. Notice that the peak of the distribution is at speed ν_o.

Fig 3.6(a)

(d) Consider particles confined to move in a plane or in one dimension (on a line). What is their speed distribution P(ν) and at what speed does it peak?

n = f NdVp.