Consider a nonrelativistic fluid that, in the neighborhood of the origin, has fluid velocity with ij

Consider a nonrelativistic fluid that, in the neighborhood of the origin, has fluid velocity

with σ_ij symmetric and trace-free. As we shall see in Sec. 13.7.1, this represents a purely shearing flow, with no rotation or volume changes of fluid elements; σ_ij is called the fluid’s rate of shear. Just as a gradient of temperature produces a diffusive flow of heat, so the gradient of velocity embodied in σ_ij produces a diffusive flow of momentum (i.e., a stress). In this exercise we use kinetic theory to show that, for a monatomic gas with isotropic scattering of atoms off one another, this stress is

with the coefficient of shear viscosity

where ρ is the gas density, λ is the atoms’ mean free path between collisions, and

is the atoms’ rms speed. Our analysis follows the same route as the analysis of heat conduction.

(a) Derive Eq. (3.85b) for the shear viscosity, to within a factor of order unity, by an order-of-magnitude analysis.

(b) Regard the atoms’ distribution function N as being a function of the magnitude p and direction n of an atom’s momentum, and of location x in space. Show that, if the scattering is isotropic with cross section σ_s and the number density of atoms is n, then the Boltzmann transport equation can be written as

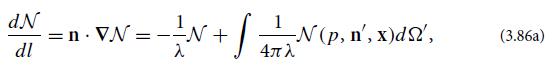
where λ = 1/nσ_s is the atomic mean free path (mean distance traveled between scatterings) and l is distance traveled by a fiducial atom.

(c) Explain why, in the limit of vanishingly small mean free path, the distribution function has the following form:

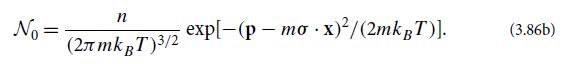
(d) Solve the Boltzmann transport equation (3.86a) to obtain the leading-order correction N₁ to the distribution function at x = 0.

(e) Compute the stress at x = 0 via a momentum-space integral. Your answer should be Eq. (3.85a) with η_shear given by Eq. (3.85b) to within a few tens of percent accuracy.

Transcribed Image Text:

Vj = 0; jxj, (3.84)