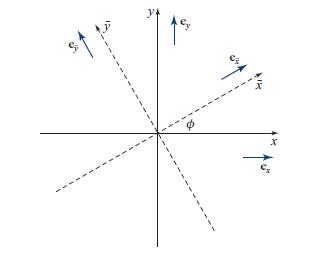
Consider two Cartesian coordinate systems rotated with respect to each other in the x-y plane as shown
Question:
Consider two Cartesian coordinate systems rotated with respect to each other in the x-y plane as shown in Fig. 1.4.
Fig. 1.4.
(a) Show that the rotation matrix that takes the barred basis vectors to the unbarred basis vectors is
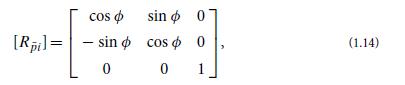
and show that the inverse of this rotation matrix is, indeed, its transpose, as it must be if this is to represent a rotation.
(b) Verify that the two coordinate systems are related by Eq. (1.13c).
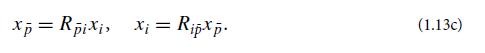
(c) Let Aj be the components of the electromagnetic vector potential that lies in the x-y plane, so that Az = 0. The two nonzero components Ax and Ay can be regarded as describing the two polarizations of an electromagnetic wave propagating in the z direction. Show that Ax̅ + iAy̅ = (Ax + iAy)e−i∅. One can show (cf. Sec. 27.3.3) that the factor e−i∅ implies that the quantum particle associated with the wave—the photon—has spin one [i.e., spin angular momentum ℏ = (Planck’s constant)/2π].
(d) Let hjk be the components of a symmetric tensor that is trace-free (its contraction hjj vanishes) and is confined to the x-y plane (so hzk = hkz = 0 for all k). Then the only nonzero components of this tensor are hxx = −hyy and hxy = hyx. As we shall see in Sec. 27.3.1, this tensor can be regarded as describing the two polarizations of a gravitational wave propagating in the z direction. Show that hx̅x̅ + ihx̅y̅ = (hxx + ihxy)e−2i∅. The factor e−2i∅ implies that the quantum particle associated with the gravitational wave (the graviton) has spin two (spin angular momentum 2ℏ); cf. Eq. (27.31).
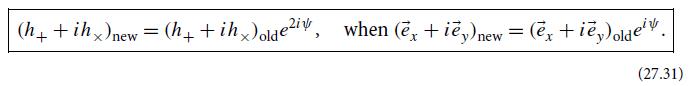
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





