Suppose that you have a noisy receiver of weak signals (e.g., a communications receiver). You are expecting a signal s(t) with finite duration and known form to come in, beginning at a predetermined time t = 0, but you are not sure whether it is present. If it is present, then your receiver’s output will be

where y(t) is the receiver’s noise, a random process with spectral density S_y(f) and with zero mean, ȳ = 0. If it is absent, then Y(t) = y(t). A powerful way to find out whether the signal is present is by passing Y(t) through a filter with a carefully chosen kernel K(t). More specifically, compute the quantity

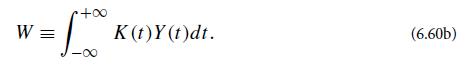
If K(t) is chosen optimally, then W will be maximally sensitive to the signal s(t) in the presence of the noise y(t). Correspondingly, if W is large, you infer that the signal was present; if it is small, you infer that the signal was either absent or so weak as not to be detectable. This exercise derives the form of the optimal filter, K(t) (i.e., the filter that will most effectively discern whether the signal is present). As tools in the derivation, we use the quantities S and N defined by

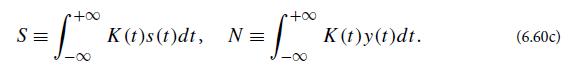
Note that S is the filtered signal, N is the filtered noise, and W = S + N. Since K(t) and s(t) are precisely defined functions, S is a number. But since y(t) is a random process, the value of N is not predictable, and instead is given by some probability distributionp1(N).We shall also need the Fourier transform K̃(f) of the kernel K(t).

(a) In the measurement being done one is not filtering a function of time to get a new function of time; rather, one is just computing a number, W = S + N. Nevertheless, as an aid in deriving the optimal filter it is helpful to consider the time-dependent output of the filter that results when noise y(t) is fed continuously into it:

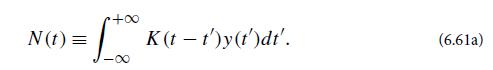
Show that this random process has a mean squared value

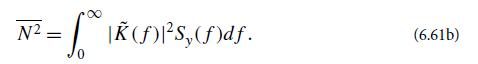
Explain why this quantity is equal to the average of the number N² computed using (6.60c) in an ensemble of many experiments:

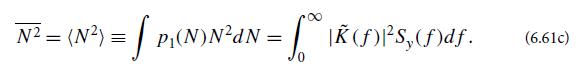
(b) Show that of all choices of the kernel K(t), the one that will give the largest value of

is Norbert Wiener’s (1949) optimal filter, whose kernel has the Fourier transform

where s̃(f ) is the Fourier transform of the signal s(t), and S_y(f ) is the spectral density of the noise. Note that when the noise is white, so S_y(f ) is independent off , this optimal kernel is just K(t) = const × s(t) (i.e., one should simply multiply the known signal form into the receiver’s output and integrate). By contrast, when the noise is not white, the optimal kernel (6.62a) is a distortion of const × s(t) in which frequency components at which the noise is large are suppressed, while frequency components at which the noise is small are enhanced.

(c) Show that when the optimal kernel (6.62a) is used, the square of the signal-to noise ratio is

(d) As an example, suppose the signal consists of n cycles of some complicated wave form with frequencies spread out over the range f_o/2 to 2f_o with amplitude ∼ A for its entire duration. Also suppose that S_y is approximately constant (near white noise) over this frequency band. Show that

so the amplitude signal to noise increases linearly with the number of cycles in the signal.

(e) Suppose (as an idealization of searches for gravitational waves in noisy LIGO data) that 

(i) We do not know the signal s(t) in advance, but we do know that it is from a set of N distinct signals, all of which have frequency content concentrated around some f_o; 

(ii) We do not know when the signal will arrive, but we search for it for a long time τ_s (say, a year);

(iii) The noise superposed on the signal is Gaussian. Show that, in order to have 99% confidence that any signal found is real, it must have amplitude signal-to-noise ratio of

where

This is so small because the Gaussian probability distribution falls off so rapidly. If the noise is non-Gaussian, then the minimum detectable signal will be larger than this, possibly much larger.

Transcribed Image Text:

Y(t) = s(t) + y(t), (6.60a)