Prove Doobs theorem. More specifically, for any Gaussian-Markov random process, show that P 2 (y 2 ,
Question:
Prove Doob’s theorem. More specifically, for any Gaussian-Markov random process, show that P2(y2, t|y1) is given by Eqs. (6.18a,b).
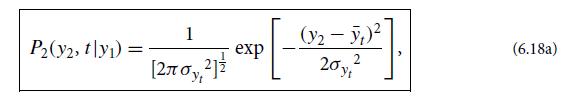
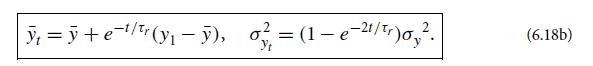
(a) Show that the Gaussian process ynew has probability distributions
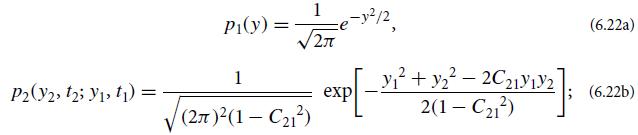
and show that the constant C21 that appears here is the correlation function C21 = Cy(t2 − t1).
(b) From the relationship between absolute and conditional probabilities [Eq. (6.4)], show that
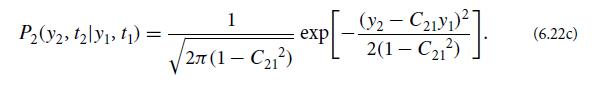
(c) Show that for any three times t3 > t2 > t1,
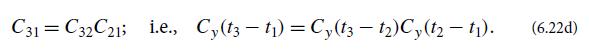
To show this, you could
(i) Use the relationship between absolute and conditional probabilities and the Markov nature of the random process to infer that
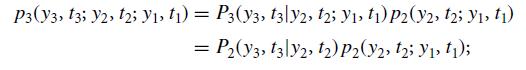
then
(ii) Compute the last expression explicitly, getting
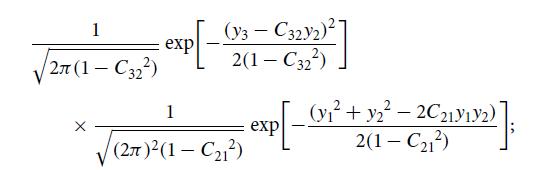
(iii) Then using this expression, evaluate

The result should be C31 = C32C21.
(d) Argue that the unique solution to this equation, with the “initial condition” that Cy(0) = σy2 = 1, is Cy(τ ) = e−τ/τr, where τr is a constant (which we identify as the relaxation time). Correspondingly, C21 = e−(t2−t1)/τr.
(e) By inserting this expression into Eq. (6.22c), complete the proof for ynew(t), and thence conclude that Doob’s theorem is also true for our original, unrescaled yold(t).
Data from Equation 6.4
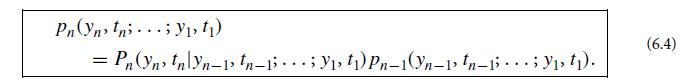
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





