Random processes can be stochastic functions of some variable or variables other than time. For example, it is conventional to describe fractional fluctuations in the largescale distribution of mass in the universe, or the distribution of galaxies, using the quantity

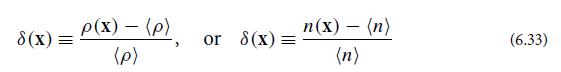
(not to be confused with the Dirac delta function). Here ρ(x) is mass density and n(x) is the number density of galaxies, which we assume, for didactic purposes, to have equal mass and to be distributed in the same fashion as the dark matter. This δ(x) is a function of 3-dimensional position rather than 1-dimensional time, and (·) is to be interpreted conceptually as an ensemble average and practically as a volume average (ergodic hypothesis!).

(a) Define the Fourier transform of δ over some large averaging volume V as

and define its spectral density by

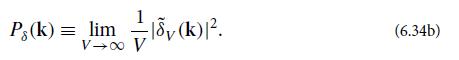
Show that the two-point correlation function for cosmological density fluctuations, defined by

is related to P_δ(k) by the following version of the Wiener-Khintchine theorem:

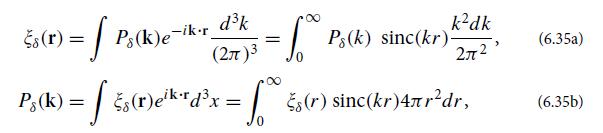
where sinc x ≡ sin x/x. In deriving these expressions, use the fact that the universe is isotropic to infer that ξ_δ can depend only on the distance r between points and not on direction, and P_δ can depend only on the magnitude k of the wave number and not on its direction.

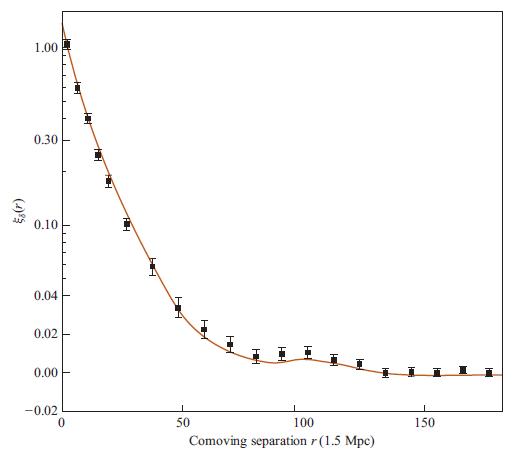
(b) Figure 6.9 shows observational data for the galaxy correlation function ξ_δ(r). These data are rather well approximated at r

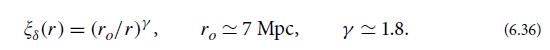
(Here 1 Mpc means 1× 10⁶ parsecs or about 3 × 10⁶ light-years.) Explain why this implies that galaxies are strongly correlated (they cluster together strongly)on length scales 

(Recall that the distance between our Milky Way galaxy and the nearest other large galaxy, Andromeda, is about 0.8 Mpc.) Use the Wiener-Khintchine theorem to compute the spectral density P_δ(k) and then the rms fractional density fluctuations at wave number k in bandwidth △k = k. From your answer, infer that the density fluctuations are very large on lengthscales(c) As a more precise measure of these density fluctuations, show that the variance of the total number N(R) of galaxies inside a sphere of radius R is

Evaluate this for the spectral density P_δ(r) that you computed in part (b).

Fig 6.9.

Transcribed Image Text:

8(x) = p(x) - (p) (p) or 8(x) n(x) - (n) (n) (6.33)