A current I₀ flows up the z-axis from z = z₁ to z = z₂ as shown below.

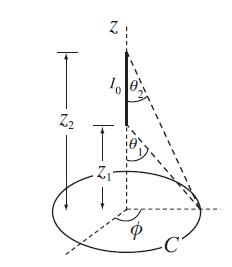
(a) Use the Biot-Savart law to show that the magnetic field in the z = 0 plane is

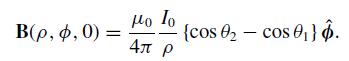
(b) Symmetry and the Coulomb gauge vector potential show that A = A_z(ρ, z) ẑ and B = ∇ × A = Bφ(ρ, z). However, an origin-centered, circular Amp`erian loop C in the z = 0 plane gives B = 0, rather than the answer obtained in part (a). The reason is that the current segment I<sub>0</sub> does not satisfy ∇ · j = 0. To reconcile Biot Savart with Amp`ere, supplement I₀ by the current densities

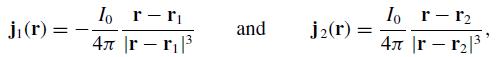
where r₁ = (0, 0, z₁) and r₂ = (0, 0, z₂). Describe j₁(r) and j₂(r) in words and show quantitatively that they, together with I₀, form a closed circuit.
(c) Using I₀, j₁, and j₂ as current sources, apply Amp`ere’s law in integral form to recover the formula derived in part (a).
(d) Show that the addition of j₁(r) and j₂(r) does not spoil the Biot-Savart calculation of part (a).

- Z lo 16 1 1 -C