Backward The success of the “working backward” method used in the text to find the Lagrangian for a charged particle in an external electromagnetic field is not obvious. Helmholtz proved in 1887 that a Lagrangian description exists for a general position- and velocity-dependent force with Cartesian components Fk = Fk(r, ṙ, t) if

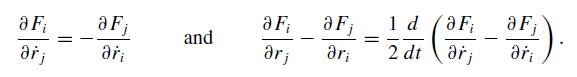
(a) Show that the first Helmholtz condition implies that ∂²F_i/∂ṙ_j∂ṙ_k = 0. Integrate this equation explicitly and deduce that F has the Coulomb-Lorentz form

where P(r, t) and Q(r, t) are arbitrary vector functions of the coordinates and time only.

(b) Show that the second Helmholtz condition implies that P and Q satisfy the homogeneous “Maxwell” equations

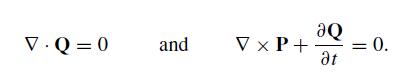
(c) The equation of motion for a particle subject to no external forces but in a reference frame that rotates with angular velocity ω with respect to an inertial reference frame is

The second and third terms on the right-hand side are the familiar Coriolis and centrifugal forces. Show that the total force for this problem satisfies both Helmholtz relations. Identify the electric-like field P and the magnetic-like field Q. Confirm by explicit calculation that these fields satisfy the homogeneous “Maxwell” equations.

Transcribed Image Text:

aF₁ ar; aF; ar: and a F; ar aFi ar; = 1 d 2 dt a F: arj aF; ar: