If the photon had a mass m, Gauss law with E = changes from 2
Question:
If the photon had a mass m, Gauss’ law with E = −∇ϕ changes from ∇2ϕ = −ρ/ ε0 to an equation which includes a lenght L = − ђ/mc:
Experimental searches for m use a geometry first employed by Cavendish where a solid conducting sphere and a concentric, conducting, spherical shell (radii r1 < r2) are maintained at a common potential Ф by an infinitesimally thin connecting wire. When m = 0, all excess charge resides on the outside of the outer shell; no charge accumulates elsewhere.
(a) Use the substitution ϕ(r) = u(r)/r to solve the equation above in the space between the conductors. Find also the electric field in this region.
(b) Use the generalization of Gauss’ law for E implied by the foregoing equation for ϕ to find the charge Q of the conducting ball.
(c) Show that, to leading order when L→∞,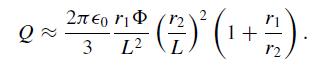
Step by Step Answer:






