Question: Let B(x, z) be the magnetic field produced by a surface current density K(y, z) = K(z) y confined to the x = x 0

Let B(x, z) be the magnetic field produced by a surface current density K(y, z) = K(z) ŷ confined to the x = x₀ plane.

(a) Show that the Biot-Savart law for this situation reduces to a one dimensional convolution integral for each component of B.
(b) Confine your attention to x 0 and show that

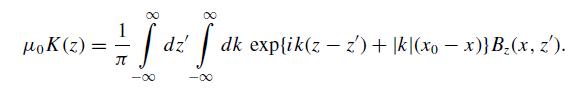
(2) - az dk dz' = 88 - f dk exp{ik(zz) +

(c) Why does the single component Bz(x, z) evaluated at one (arbitrary) value of x 0 provide enough information to determine j (z)?

(2) - az dk dz' = 88 - f dk exp{ik(zz) + k|(xox)} B(x, z).

Step by Step Solution

★★★★★

3.25 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a b Define the Fourier transform pairs c Br 440 Kx rr r r ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Electrodynamics Questions!

A long, straight wire carrying a current of 200 A, runs trough a cubical wooden box, entering and leaving through holes in the centres of opposite faces (Fig). The length of each side of the e- box...

This problem leads you through a study of electric and magnetic fields as viewed by two different observers, that is, in two different reference frames. Suppose a charge q 1 is moving with a constant...

A power line carries a current of 95 A along the tops of 8.5-m-high poles. What is the magnitude of the magnetic field produced by this wire at the ground? How does this compare with the Earths field...

Problem 1 : A surface current density K exists on a hollow sphere of radius a centered at the origin. Find the magnetic field at the origin. Hint: Ignore the magnetic field due to the filament...

4. Consider an innitely long cylinder with a circular cross section of radius R. Let its symmetric axis be the z axis and set up the usual cylindrical coordinate system. Surface currents run parallel...

Two conducting strips, having infinite length in the z direction, lie in the xz plane. One occupies the region d/2

\f\f3. a) potential function = x2 +y 2 +z 2 ; magnetic force M = y 2 zi+z 2 xj+x2 yk i) Grad = i+ j+ k x y z Note that : = 2x = 2y = 2z x y z Hence, Grad = 2xi + 2yj + 2zk M M M ii) Div M = + + x y z...

Problem # 1 ( 4 pts each 2 0 pts total ) : a ) vec ( E ) ( z , t ) = E 0 [ h a t ( x ) c o s ( t + k z ) + hat ( y ) c o s ( t + k z - 2 ) ] is . . . Linearly polarized in the hat ( x ) direction...

When dealing with the classical Hall effect and the quantum Hall effect, the magnetic field B, is often pointed along the z direction perpendicular to the sample plane. Now consider that the magnetic...

1. The gravitational force field created by the mass M and acting on the mass m is F = -GMm 3, where r(x, y, z) = (x, y, z). In the following calculations, assume you are using units where GMm = 1....

Determine the stability of amplifier, given the open loop transfer function. A two pole feedback amplifier with an open-loop transfer function is given as 100 A(s) = where s=jw and w=2af. 1+ 104 (a)...

Considering the market risks of interest rate, foreign exchanges, and commodity price risk, assess the risk that you believe may have the most significant impact on a firm. Indicate how this risk can...

4. Consider the data given in Problem 1. Suppose it costs Rs 2 to increase production by one unit and Re 1 to decrease production by one unit. How will you modify the model formulated in Problem 2 to...

Montner et al. (A-46) conducted studies to test the effects of glycerol-enhanced hyperhydration (GEH) on endurance in cycling performance. The 11 subjects, ages 2240 years, regularly cycled at least...

Suppose it is known that the graph of the function y = ax 3 + bx 2 + cx + d passes through four given points (x i , y i ), i = 1, 2, 3, 4. Write a userdefined function that accepts these four points...

Create an anonymous function for 10e -2x and use it to plot the function over the range 0 x 2.

Create an anonymous function for 20x 2 - 200x + 3 and use it a. To plot the function to determine the approximate location of its minimum b. With the fminbnd function to precisely determine the...

12/31/2020 year-end balance sheet retained earnings-Unappropriated: $7,481,904 12/31/2021 year end balance sheet Retained earnings-unappropriated:$ ? please find the Retained earnings on 12/31/2021...

Jeanlouis, Inc., manufactures and sells two products: Product D0 and Product D5. The company has an activity-based costing system with the following activity cost pools, activity measures, and...

Pantanal, Inc., manufactures car seats in a local factory. For costing purposes, it uses a first-in, first-out (FIFO) process costing system. The factory has three departments: Molding, Assembling,...