Let the dielectric function () = 0 n 2 () characterize a macroscopic sphere of matter
Question:
Let the dielectric function (ω) = ϵ0n2(ω) characterize a macroscopic sphere of matter composed of N electrons. If the wavelength of the incident field is large compared to the sphere radius a, it is legitimate to use a quasistatic approximation. This problem equates two expressions for the polarization P(t) to find ϵ(ω).
(a) Solve a quasi-electrostatic boundary value problem to find P(t) when the sphere is exposed to an external electric field E0 cos(ωt).
(b) Let the sphere have polarization P cos ωt. Cut out a tiny sphere (of vacuum) around any one of its electrons and show that P(t) produces no force on the electron. Find the dipole moment of the electron induced by the electric field in part (a) and a spring-like force (with natural frequency ω0) which holds the electron at the center of its vacuum sphere. Sum the moments from all the electrons and equate the resulting polarization to the result of part (a) to get the Lorenz-Lorentz formula,
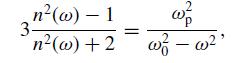
where 4 /3 π a3 n0 = N and ω2p = n0e2/mϵ0.
(c) For a neutral plasma, we suppose that the N electrons are distributed in a sphere of uniform positive charge. The forces on any one electron come from
(i) the electric field due to the positively charged sphere;
(ii) the (quasistatic) Coulomb interaction with the other N − 1 electrons; and
(iii) the external electric field. Show that force (ii) drops out in Newton’s equation of motion for the total dipole moment P = −(e/V ) ΣNk =1 rk where V = 4 / 3 πa3. Solve the equation of motion for P and equate this to the result in part (a) to get the high-frequency Drude formula,
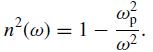
Step by Step Answer:






