The figure below shows a current I which flows down the z-axis from infinity and then spreads out radially and uniformly to infinity in the z = 0 plane.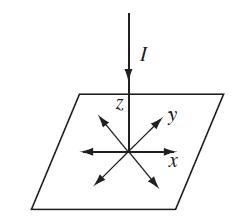

(a) The given current distribution is invariant to reflection through the y-z plane. Prove that, when reflected through this plane, the cylindrical components of the magnetic field transform from

(b) Compare the results of part (a) to the transformation of B to B̃, where the latter is a π rotation around the z-axis that also leaves the current invariant. Use this and any other symmetry argument you need to conclude that  everywhere.

(c) Use the results of part (b) and Ampere’s law to find the magnetic field everywhere.

(d) Check explicitly that your solution satisfies the magnetic field matching conditions at the z = 0 plane.

X I N