A rotation of a set of rectangular cartesian axes (Ox 1 x 2 x 3 ) to

Question:

A rotation of a set of rectangular cartesian axes Φ(Ox₁x₂x₃) to a set Φ´(Ox´₁ x´₂ x´₃) is described by the matrix L = (l_ij) (i, j = 1, 2, 3), where l_ij is the cosine of the angle between Ox´_i and Ox_j. Show that L is such that LL^T = I and that the coordinates of a point in space referred to the two sets of axes are related by

X' = LX where X' = [x' x x3] and X = [X X X3]. Prove that x + x + x = x + x + x} Describe the relationship

The axes Φ´ are now rotated through 45° about Ox´₃ in the sense from Ox´₁ to Ox´₂ to form a new set Φ´´. Show that the angle θ between the line OP and the axis Ox´´₁, where P is the point with coordinates (1, 2, –1) referred to the original system Φ, is

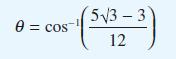
0 = cos 53-3 12