Show that a tridiagonal matrix can be written in the form

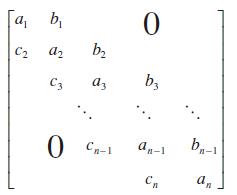
A matrix that has zeros in every position below the diagonal is called an upper-triangular matrix and one with zeros everywhere above the diagonal is called a lower-triangular matrix. A matrix that only has non-zero elements in certain diagonal lines is called a banded matrix. In this case we have shown that a tridiagonal matrix can be written as the product of a lower-triangular banded matrix and an upper-triangular banded matrix.