Show that if is a complex cube root of unity, then 2 + +

Show that if ω is a complex cube root of unity, then ω² + ω + 1 = 0. Deduce that

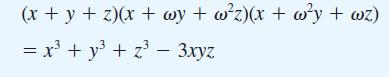
Hence show that the three roots of

Express the remaining two roots in terms of u, v and ω and find the condition that all three roots are real.

Transcribed Image Text:

(x + y + z)(x + wy + wz)(x + wy + wz) = = x3 + y3 + z3 - 3