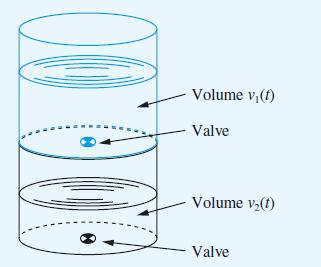
Two cylindrical water tanks are connected as shown in Figure 11.22. Initially there are 250 litres in the top tank and 50 litres in the bottom tank. At time t = 0 the valve between the two tanks and the valve at the bottom of the lower tank are opened. The flowrate through each of these valves is proportional to the volume of water in the tank immediately above the valve, the constant of proportionality being 0.1 for both valves. Denoting the volume in the top tank by v₁ and the volume in the bottom tank by v₂, show that the following differential equations are satisfied:

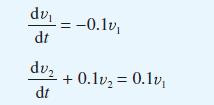
(a) Use Laplace transforms to determine v₁ and v₂.

(b) Find the time taken for the volume of water in the top tank to reach 10% of its starting value.

Figure 11.22

Transcribed Image Text:

dv dt dv dt -0.1v + 0.1v = 0.1v