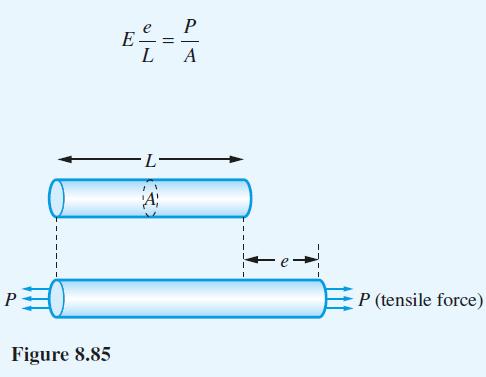
When a homogeneous bar of constant crosssectional area A (see Figure 8.85) is under uniformly distributed tensile
Question:
When a homogeneous bar of constant crosssectional area A (see Figure 8.85) is under uniformly distributed tensile stress, the elongation in the direction of the stress for a material obeying Hooke’s law is given by stress = E × strain where E is Young’s modulus, the stress is the applied force per unit area and the strain is the ratio of the elongation to the unstretched length of the bar. That is,
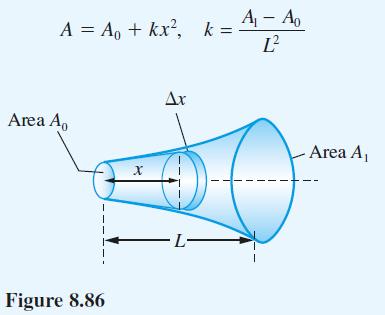
Consider a bar of circular cross-section whose diameter varies along its length as shown in Figure 8.86, so that
By considering the elongation of an element of thickness Δx of the bar, show that the total elongation of the bar under the tensile force P is
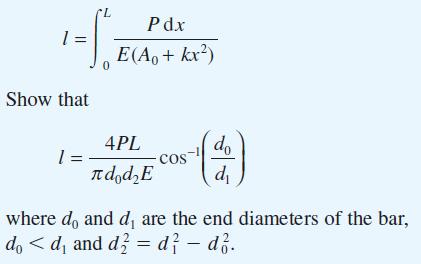
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





