(a) Demonstrate that Eq. (6.10) defines a generator of \(\mathrm{SO}(2)\) by examining the \(2 \mathrm{D}\) rotation matrix (6.3) for an infinitesimal rotation \(d \phi\).

(b) Show that Eqs. (6.3) and (6.9) are equivalent by expanding the exponential in Eq. (6.9) to all orders.

Data from Eq. 6.3

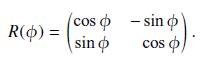
Data from Eq. 6.9

Data from Eq. 6.10

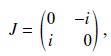
R() = - (cos sin o & sin cos