Assume a 2D lattice with islands of superconductivity surrounded by regions of insulating behavior. Within each SC island patch \(i\), assume a set of electron Cooper pairs having the same wavefunction phase that can be approximated as bosons. A simple Hamiltonian describing this system is given by the Bose-Hubbard model 

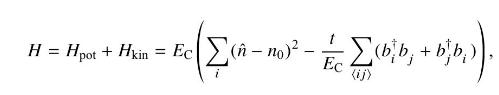
where \(b_{i}^{\dagger}\) creates a Cooper pair on patch \(i\) and \(b_{i}\) annihilates it, \(n_{0}\) is the average Cooper pair density, \(E_{\mathrm{C}}\) is the energy cost to convert an isolated Cooper pair into charge carriers in a conductor, \(t\) is the energy associated with a Cooper pair hopping between adjacent patches \(i\) and \(j\), and \(\langle i jangle\) indicates that the summation is only over patches \(i\) and \(j\) that are nearest neighbors. Describe physically the competing ground state tendencies of this Hamiltonian as \(t / E_{\mathrm{C}}\) is varied. Prove that the kinetic and potential energies do not commute, suggesting that there should be a critical point at a quantum phase transition between \(\mathrm{SC}\) and insulating states as \(t / E_{\mathrm{C}}\) is varied.

Transcribed Image Text:

HHpot +Hkin = Ec == (n- ( - no) - - bbbb Ec (ij)