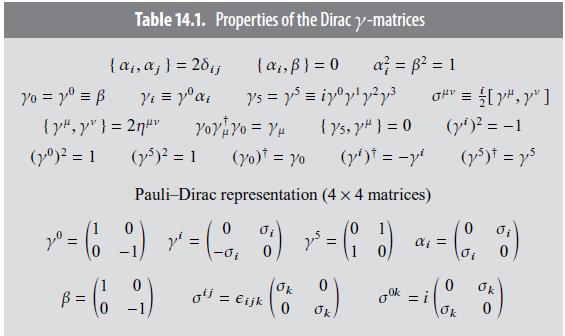
In the Pauli-Dirac representation of Table 14.1, a suitable charge conjugation operator is \(C=i \gamma^{2} \gamma^{0}\). Show that \(C\) is given explicitly by the matrix

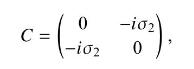
in this representation. Verify by matrix multiplication the matrices for \(\gamma^{5}\) shown in Table 14.1 for the Pauli-Dirac and Weyl (chiral) representations. Hint: A useful identity for Pauli matrices is \(\sigma_{1} \sigma_{2} \sigma_{3}=i \mathrm{I}^{(2)}\), where \(\mathrm{I}^{(2)}\) is the \(2 \times 2\) unit matrix.

Data from Table 14.1

Transcribed Image Text:

(201- 201-) == C =