Matrices are central to representation theory. If \(A, B, C\), and \(D\) are square, invertible, \(n \times n\) matrices with complex entries, prove the following useful properties.

a. The trace of a matrix is invariant under similarity transforms, \(\operatorname{Tr}\left(B A B^{-1}\right)=\operatorname{Tr} A\). Hint: Written out with indices, \(\left(B A B^{-1}\right)_{i j}=B_{i \ell} A_{\ell k} B_{k j}^{-1}\).

b. Products of exponentiated matrices behave in the expected way, provided that the matrices commute with each other: \(e^{A} e^{B}=e^{A+B}\) if \([A, B]=0\). (See the BCH formula quoted in Problem 3.15 for the case \([A, B] eq 0\).)

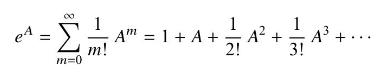
for a matrix \(A\).

c. The exponential \(e^{A}\) has eigenvalues \(e^{\lambda_{1}}, e^{\lambda_{2}}, \ldots, e^{\lambda_{n}}\) if the matrix \(A\) has eigenvalues \(\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}\).

d. The determinant of an exponentiated matrix is the exponentiated trace of the matrix, det \(e^{A}=e^{\operatorname{Tr} A}\). The determinant of a matrix is the product of its eigenvalues and the trace of a matrix is the sum of its eigenvalues.

e. The trace of a product of two square matrices is independent of the order of multiplication: \(\operatorname{Tr}(A B)=\operatorname{Tr}(B A)\).

f. Cyclic property of the trace: The trace of a matrix product is invariant under cyclic permutation of the factors in the product.

g. The hermitian conjugate of a matrix product is the product of the hermitian conjugates for each matrix, in reverse order. For example, \((A B C D)^{\dagger}=D^{\dagger} C^{\dagger} B^{\dagger} A^{\dagger}\). Hint: The hermitian conjugate of a matrix is the transpose of its complex conjugate, so the matrix elements for \(M^{\dagger}\) are given by \(\left(M^{\dagger}\right)_{i j}=\left(M_{j i}\right)^{*}\).

h. The inverse of a matrix product is the product of the inverses for each matrix, in reverse order. For example, \((A B C D)^{-1}=D^{-1} C^{-1} B^{-1} A^{-1}\).

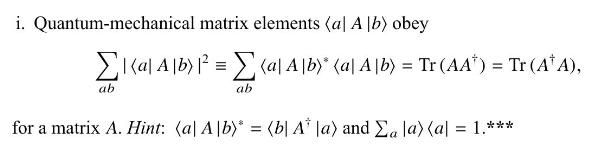
Data from Problem 3.15

Show that the group-element commutator \(R_{y}(\delta \theta) R_{x}(\delta \theta) R_{y}^{-1}(\delta \theta) R_{x}^{-1}(\delta \theta)\), is related to the generator commutator \(\left[J_{x}, J_{y}\right]\) by

where the group elements and generators are related by \(R_{x}(\theta)=\exp \left(i J_{x} \theta\right)\) and \(R_{y}(\theta)=\exp \left(i J_{y} \theta\right)\) for a rotation angle \(\theta\). Keep the first three terms of

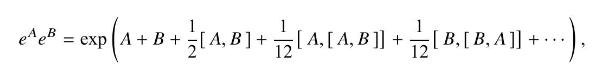
which is called the Baker-Campbell-Hausdorff (BCH) formula.

Transcribed Image Text:

eA = m! m=0 A" = 1+ A+ 2! 3!