Prove the useful identity employed in Eq. (14.20) that \(e^{i L \phi}=\cosh \phi+i L \sinh \phi\). Expand the exponential in a power series and compare the odd and even terms to the power series expansions of \(\cosh \phi\) and \(\sinh \phi\).

Data from Eq. 14.20

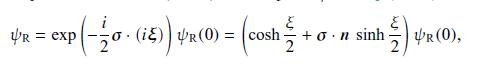
2 VR = exp Xxp(-120 - (i) Y/R( | VR (0) = (co cosh +.n sinh 1) VR (0),