Suppose that (D^{(alpha)}) and (D^{(beta)}) are irreps of a compact simple group with dimensions (n_{alpha}) and (n_{beta}),
Question:
Suppose that \(D^{(\alpha)}\) and \(D^{(\beta)}\) are irreps of a compact simple group with dimensions \(n_{\alpha}\) and \(n_{\beta}\), respectively, and basis vectors \(x_{i}\) and \(y_{i}\), respectively. If the basis vectors \(\boldsymbol{x}=\left(x_{1}, x_{2}, \ldots\right)\) and \(\boldsymbol{y}=\left(y_{1}, y_{2}, \ldots\right)\) describe independent degrees of freedom for the system, investigate the transformation properties of the two-index quantities \(x_{n} y_{n}\) and show that they transform as the matrix \(C_{i k, j l}\) in Eq. (2.28).
Data from Eq. (2.28)
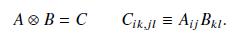
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun
Question Posted:





