A one-dimensional simple harmonic oscillator of angular frequency is acted upon by a spatially uniform but
Question:
A one-dimensional simple harmonic oscillator of angular frequency ω is acted upon by a spatially uniform but time-dependent force (not potential)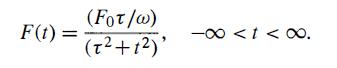
At t = -∞, the oscillator is known to be in the ground state. Using the timedependent perturbation theory to first order, calculate the probability that the oscillator is found in the first excited state at t = +∞.
Challenge for experts: F(t) is so normalized that the impulse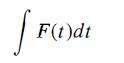
imparted to the oscillator is always the same-that is, independent of τ; yet for r ≫ 11 w, the probability for excitation is essentially negligible. Is this reasonable? [Matrix element of x:
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
To calculate the probability of the onedimensional simple harmonic oscillator being in the first exc...View the full answer
Answered By
Abdul Wahab Qaiser
Before working at Mariakani, I volunteered at a local community center, where I tutored students from diverse backgrounds. I helped them improve their academic performance and develop self-esteem and confidence. I used creative teaching methods, such as role-playing and group discussions, to make the learning experience more engaging and enjoyable.
In addition, I have conducted workshops and training sessions for educators and mental health professionals on various topics related to counseling and psychology. I have presented research papers at conferences and published articles in academic journals.
Overall, I am passionate about sharing my knowledge and helping others achieve their goals. I believe that tutoring is an excellent way to make a positive impact on people's lives, and I am committed to providing high-quality, personalized instruction to my students.
0 Reviews
10+ Question Solved
Related Book For 
Question Posted:
