Consider the setting of section 12.3 .4 but now allow for multiple risky assets (j=1, ldots, J).
Question:
Consider the setting of section 12.3 .4 but now allow for multiple risky assets \(j=1, \ldots, J\). The speculators' budget constraint and margin constraint are now given by \(W_{t}=W_{t-1}+\) \(\sum_{j=1}^{J}\left(p_{t}^{j}-p_{t-1}^{j}ight) x_{t-1}^{j}+\eta_{t}\) and \(\sum_{j=1}^{J} \tilde{m}_{t}^{j}\left|x_{t}^{j}ight| \leq W_{t}\), respectively. Customers' quantity demanded of asset \(j\) at date 1 is \(D_{1}^{j}\left(\Lambda_{1}^{j}, Z_{1}^{j}ight)\), where \(\Lambda_{1}^{j} \equiv v_{1}^{j}-p_{1}^{j}\). The speculators' date- 1 wealth shock \(\eta_{1}\) has zero mean and is uncorrelated with the demand shocks \(Z_{1}^{j}\).
Assume \(p_{1}^{j} eq v_{1}^{j}\) for at least some \(j\), so that speculators are capital-constrained at date 1 (with \(W_{1}>0\) ).
(a) Derive speculators' demand \(x_{1}^{j}\) for each asset. Hint: Explain why speculators only trade assets with the highest \(\left|\Lambda_{1}^{j}ight| / \tilde{m}_{1}^{j}\).
(b) Denote speculators' date- 1 value function by \(J_{1}\left(W_{1}ight)=\mathrm{E}_{1}\left[W_{2}ight]\). Their date- 1 shadow cost of capital \(\varphi_{1}\), a measure of funding illiquidity, is defined through \(\varphi_{1} W_{1}=J_{1}\left(W_{1}ight)\). Express \(\varphi_{1}\) in terms of \(\Lambda_{1}^{j}\) and \(\widetilde{m}_{1}^{j}, j=1, \ldots, J\).
(c) Express each asset's market illiquidity, \(\left|\Lambda_{1}^{j}ight|\), in terms of \(\varphi_{1}, \widetilde{m}_{1}^{j}\), and parameters of the model.
(d) Now consider an additional initial period \(t=0\) with a margin constraint on speculators \(\sum_{j=1}^{J} \widetilde{m}_{0}^{j}\left|x_{0}^{j}ight| \leq W_{0}\). Assume that speculators have unlimited liability, and in particular \(J_{1}\left(W_{1}ight)=\varphi_{1} W_{1}\) for all values of \(W_{1}\) (including negative ones), with \(\varphi_{1}\) from part (b). This assumption raises the possibility that speculators do not trade to their constraint at date 0 if their wealth is high enough.
Assuming that speculators are unconstrained at \(t=0\), show that \(\varphi_{1} / \mathrm{E}_{0}\left[\varphi_{1}ight]\) functions as an SDF in the economy. Explain intuitively why speculators choose to not trade to their constraint even though they are risk-neutral. Show that their date-0 cost of capital \(\varphi_{0}\), defined through \(\varphi_{0} W_{0}=J_{0}\left(W_{0}ight)=\mathrm{E}_{0}\left[W_{2}ight]\), equals \(\mathrm{E}_{0}\left[\varphi_{1}ight]\).
(e) Now suppose that speculators' wealth \(W_{0}\) is low enough that speculators are constrained at \(t=0\). Derive their date- 0 cost of capital, \(\varphi_{0}\).
Data from section 12.3.4

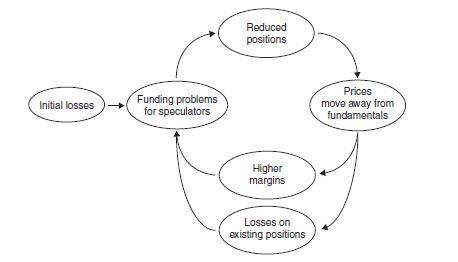





Step by Step Answer:

Financial Decisions And Markets A Course In Asset Pricing
ISBN: 9780691160801
1st Edition
Authors: John Y. Campbell





