Consider the dynamics of a passive scalar (0 leq Phi(t, mathbf{x}) leq 1) in a turbulent flow.
Question:
Consider the dynamics of a passive scalar \(0 \leq \Phi(t, \mathbf{x}) \leq 1\) in a turbulent flow. Specialize the transport pde (11.52) for the \(\operatorname{Pdf} f_{N}\left(\varphi_{1}, \ldots, \varphi_{N}\right)\) of \(N\) scalars to the Pdf \(f(\varphi)\) for a single scalar \(\Phi\) and show that, the diffusive term in scalar space has negative diffusivity. You may assume that the scalar sources depend locally on the scalars only \(Q\left(\varphi(1), \ldots, \varphi^{(N)}\right)\) and not on velocity. The following model expression for the diffusive term in scalar space (Curl [11]) is suggested
\[ -\frac{\partial^{2}}{\partial \varphi^{2}}\left\langle\frac{1}{\operatorname{ScRe}} abla \Phi \cdot abla \Phi \delta(\Phi(t, \mathbf{x})-\varphi)\rightangle \approx \frac{c}{\tau}\left[4 \int_{0}^{\varphi} d \varphi^{\prime} f\left(\varphi+\varphi^{\prime}\right) f\left(\varphi-\varphi^{\prime}\right)-f(\varphi)\right] \]
to mimic the effect of the diffusive term, where the time scale \(\tau>0\) is independent of \(\Phi\) and \(c\) is a positive constant. Show that this expression
11.3.1 leaves normalization and mean unchanged;
11.3.2 reduces the variance.
pde (11.52)
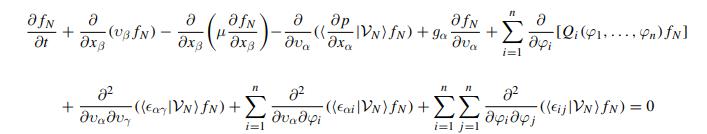
Step by Step Answer:

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann





