Determine the material deformation gradient as measured by deformation gradient and deformation rate (velocity gradient) for the
Question:
Determine the material deformation gradient as measured by deformation gradient and deformation rate (velocity gradient) for the restricted Euler system. The restricted Euler flow is governed by (2.122) introduced in Sect. 2.7.
(4.1) Derive the pde for the deformation gradient \(F_{\alpha \beta}\) in mixed formulation using the spatial deformation rate \(A_{\alpha \beta}\).
(4.2) Derive the transport pde for the deformation rate \(A_{\alpha \beta}\) in the spatial description.
(4.3) Establish the odes for the non-trivial invariants \(Q\) (2.114) and \(R\) (2.115). Hint: Use the Cayley-Hamilton theorem
\[ A_{\alpha \gamma} A_{\gamma \delta} A_{\delta \beta}+Q A_{\alpha \beta}+R \delta_{\alpha \beta}=0 \]
valid for traceless matrices \(A_{\alpha \beta}\).
(4.4) Solve the odes for the invariants \(Q\) and \(R\) and plot the results in the \(R-Q\) phase plane for \(-8 \leq R, Q \leq 8\). Show that there appears a cusp singularity (defined as \(x^{2}-y^{3}=0\) for \(x=y=0\) in standard form) at the origin.
Sect. 2.7

Eq (2.122)
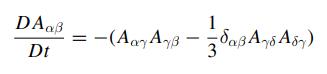
Step by Step Answer:

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann




