Compute the solution (Psi) of the pde (20.26) for the Chaplygin-Lamb dipole streamfunction [ frac{partial^{2} Psi}{partial r^{2}}+frac{1}{r}
Question:
Compute the solution \(\Psi\) of the pde (20.26) for the Chaplygin-Lamb dipole streamfunction
\[ \frac{\partial^{2} \Psi}{\partial r^{2}}+\frac{1}{r} \frac{\partial \Psi}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2} \Psi}{\partial \theta^{2}}=-\omega \]
for \(\omega(r, \theta)=n^{2}(\Psi(r, \theta)-\lambda\), where \(\lambda\) is an arbitrary constant, requiring continuity of velocity across the cylinder surface \(r=a\). Plot streamlines and vorticity within the cylinder and the vorticity profiles for several values of \(\lambda\) along the vertical axis \(\theta=\frac{\pi}{2}\).
pde (20.26)
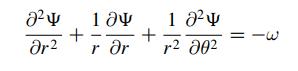
Step by Step Answer:
Related Book For 

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann
Question Posted:




