2.64. Complex normal distribution. Let (X', Y')' have a normal distribution with mean vector (,ix, ,iy)' and covariance matrix

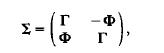
where f is positive definite and III = - III' (skew symmetric). Then. Z = X + iY is said to have a complex normal distribution with mean 6 = I~x +il J.y and covariance matrix G(Z - 6)(Z - 6)* = P = Q + iR, where Z* =X' - iY'. Note that P is Hermitian and positive definite.

(a) Show Q = 2r and R = 2111.

(b) St,ow IPI 2 = 1211. [Hint: If+illli = If-illll.]

(c) Show

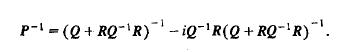Note that the inverse of a Hermitian matrix is Hermitian.

(d) Show that the density of X and Y can be written

x-(6 == (6 +"), r