5.7. Let {Xn,t,An,t} be a martingale difference sequence. Suppose the Lindeberg condition: Xn t=1 E{X2 n,t(|Xn,t| >
Question:
5.7. Let {Xn,t,An,t} be a martingale difference sequence. Suppose the Lindeberg condition:
Xn t=1 E{X2 n,tχ(|Xn,t| > ε)} → 0, (n → ∞), for every ε > 0.
Then, show the following (i) and (ii):
(i) max 1≤t≤n
|Xn,t| p→
0,
(ii) there exists M > 0 satisfying
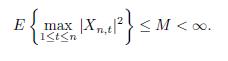
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Optimal Statistical Inference In Financial Engineering
ISBN: 9781584885917
1st Edition
Authors: Masanobu Taniguchi, Junichi Hirukawa, Kenichiro Tamaki
Question Posted:






