A convenient way to visualize the evolution of a two-dimensional system is to make a phase plane plot. We will do more of this type of calculation in Chapter 5. For now, we would like to see how the solution to the system of equations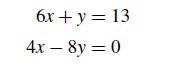

changes when you use Jacobi’s method with an initial guess x⁽⁰⁾ = 5 and y⁽⁰⁾ = 0. Write a MATLAB program that computes the values of x^(k) and y^(k) using Jacobi’s method until the error in the solution, defined as ||x^(k)−x^(k−1)|| is less than 10⁻⁴. Your program should store all of the values of x^(k) and y^(k). In a “normal” plot, you might want to look at x vs. k or y vs. k. In the phase plane, you want to plot the points (x^(k), y^(k)) on an x, y plane and connect them by lines. The corresponding trajectory will show you how the solution method evolves to the final answer. Your program should automatically produce two plots. In the first plot, show all of the points at each value of k on an x, y plane. In the second plot, zoom in on the data close to the solution to see the details.

Transcribed Image Text:

6x + y = 13 4x - 8y = 0