In numerical methods, there are often many ways to make a calculation that give the same answer

Question:

In numerical methods, there are often many ways to make a calculation that give the same answer but have vastly different efficiencies. In this problem, we are going to consider a common calculation in molecular dynamics simulations, which requires computing the term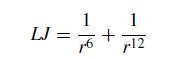 LJ 1 + 16 12

(If you are familiar with this topic, we are going to compute the Lennard–Jones potential without any prefactors.) Let us consider two particles, one located at (1, 0, 3) and another particle located at (2,−2,−1) and the following two methods for computing the LJ potential between these two particles. The input to the calculation is the positions of the two particles.

Method 1

(1) Calculate

where x is the distance x₁ −x₂ and so forth.

(2) Calculate LJ by plugging the value of r into the formula above.

Method 2

(1) Calculate r² = Δx² + Δy² + Δz².

(2) Calculate 1/r².

(3) Calculate 1/r⁶ = 1/r² × 1/r² × 1/r².

(4) Calculate 1/r¹² = 1/r⁶ × 1/r⁶.

(5) Calculate LJ by adding the results from the previous two steps.

Write aMATLAB program that determines the amount of time required to doMethod 1 and Method 2 if you do the calculation 10, 100, . . ., 10⁸ times. Look at how the calculation time increases with the number of times you need to do it – in simulations, you would make this calculation an enormous number of times. For these calculations, you should use the tic and toc commands in MATLAB to get the time. Your program should automatically produce a log-log plot of the time required versus the number of calculations.