In this problem, we will look at the two-dimensional diffusion problem with a reactive surface at one of the boundaries. The steady state PDE in the domain is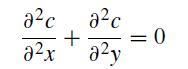

Along all of the non-reactive boundaries, we will set the concentration to unity

On the upper boundary at y = 1, we will have a first-order reaction that consumes the reactant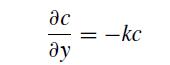

(Note that the negative sign comes from the direction of the normal vector to the reactive surface.) In the dimensionless form of this problem, the quantity k is the Dämkohler number.

Write a MATLAB program that solves this problem using 101 grid points in x and y and centered finite differences. Include a list of all of the equations that you need to

solve this problem. Even with only 101 grid points in each direction you have a very large matrix (n² = 10201), so take advantage of the sparse matrix solver. In the first use of your program, make a surface plot of the concentration as a function of position for k = 1. If you think a bit about the problem, you should be able to tell if your numerical solution makes sense or not. Include this plot with your written solution. Now have your program make a plot of the concentration at the reactive surface for the following values of the Dämkohler number: k = 0, 0.1, 0.2, 0.5, 0.75, 1, 2, 3, 5, 10, 20, 100. Include an explanation of its behavior.

Transcribed Image Text:

ac a2x + ac 8²1 = 0