This problem involves analyzing the solution of subject to the initial condition T(x, 0) = 1 and
Question:
This problem involves analyzing the solution of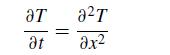
subject to the initial condition T(x, 0) = 1 and the boundary conditions T(0, t) = 0 and T(1, t) = 0. The Fourier series for the temperature is![T(x,t) = k=1 4 (2k 1) - - sin[(2k 1)x] exp[-(2k 1)22]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/1/600652f7f50b65191697611599074.jpg)
(a) Write a program that prints to the screen a formatted table of the values of the temperature at t = 0.1 for x = 0.1, 0.25, 0.5, 0.75, and 0.9 using 100 non-zero Fourier modes. Your program should use a subfunction that takes in the value of x, t, and the number of Fourier modes and returns the value of the temperature at this point. You will use this subfunction in the rest of the problem.
(b) We now want to analyze the accuracy of the solution as a function of the number of Fourier modes using 201 evenly spaced grid points between [0,1]. Let us define the “exact” solution as the value of the temperature using k = 100 Fourier modes. Write a program that computes the error in the sum using the definition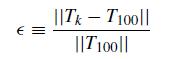
for k = 1, 2, . . . , 25. You should use the subfunction from part (a) in this calculation. Your program should automatically generate a semilog-y plot of ϵ versus k. The quantity || . . . || is a vector norm.
(c) In transport, you used graphical plots of the temperature profile to solve heat transfer problems. Here, we want to generate one such plot for our problem. Write a program that automatically generates a plot of the temperature over the domain x ∈ [0.5, 1] for the times t = 0.001, 0.005, 0.025, 0.05, 0.1, and 0.2. (Since the problem is symmetric, there is no need to worry about the other side of the slab.)
Step by Step Answer:

Numerical Methods With Chemical Engineering Applications
ISBN: 9781107135116
1st Edition
Authors: Kevin D. Dorfman, Prodromos Daoutidis




