1. Consider the following portfolio optimization problem where r R n is the expected return vector, is the return covariance matrix, and is

1. Consider the following portfolio optimization problem

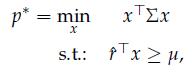
where r̂ ∈ Rⁿ is the expected return vector, is the return covariance matrix, and μ is a target level of expected portfolio return. Assume that the random return vector r follows a simplified factor model of the form  

where F ∈ R^n,k, k k is given, and f ∈ R^k is such that E{f} = 0 and E{f f ^T} = I. The above optimization problem is a convex quadratic problem that involves n decision variables. Explain how to cast this problem into an equivalent form that involves only k decision variables. Interpret the reduced problem geometrically. Find a closed-form solution to the problem.

2. Consider the following variation on the previous problem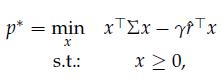where is a tradeoff parameters that weigths the relevance in the objective of the risk term and of the return term. Due to the presence of the constraint x ≥ 0, this problem does not admit, in general, a closed-form solution.

Assume that r is specified according to a factor model of the formwhere F, f and f̂ are as in the previous point, and e is an idiosyncratic noise term, which is uncorrelated with and such that  Suppose we wish to solve the problem using a logarithmic barrier method of the type discussed in Section 12.3.1. Explain how to exploit the factor structure of the returns to improve the numerical performance of the algorithm. 

p* min X X st: PT x 2, pTx