We consider a process described by difference equation

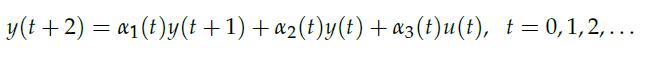
where the u(t) ∈ R is the input, y(t) ∈ R the output, and the coefficient vector a(t) ∈ R³ is time-varying. We seek to compute bounds on the vector α(t) that are (a) independent of t, (b) consistent with some given historical data.
The specific problem we consider is: given the values of u(t) and y(t) over a time period 1 ≤ t ≤ T, find the smallest ellipsoid E in R³ such that, for every t, ≤ t ≤ T, the equation above is satisfied for some a(t) ∈ ε.
1. What is a geometrical interpretation of the problem, in the space of α’s?
2. Formulate the problem as a semidefinite program. You are free to choose the parametrization, as well as the measure of the size of E that you find most convenient.
3. Assume we restrict our search to spheres instead of ellipsoids. Show that the problem can be reduced to a linear program.
4. In the previous setting, α(t) is allowed to vary with time arbitrarily fast, which may be unrealistic. Assume that impose a bound on the variation of α(t), such as ΙΙα(t + 1) – α(t)ΙΙ₂≤ β, where β > 0 is given. How would you solve the problem with this added restriction?

Transcribed Image Text:

y(t + 2) = x₁(t)y(t+1) + a2(t)y(t) + x3 (t)u(t), t= 0,1,2,...