Choice based conjoint studies (see Section 6.7 for an example and de-

scription of conjoint analysis) are frequently used in marketing research.

In choice based conjoint studies, potential customers are asked to choose among several alternatives. The alternatives are combinations of levels of several product characteristics. The response for each combination of prod-

uct characteristics is a count of the number of potential customers who choose that alternative. Analysis of the data helps marketing researchers determine what product characteristics have the most in uence on cus-

tomer choices and what mix of alternatives they should oer in order to satisfy the needs of the market. Consider the following scenario described by Street and Burgess (2007). Researchers want to study how the attributes of a take-out pizza outlet aect consumer choice of where they buy their pizza. The table below lists the product characteristics (i.e., factors in ex-

perimental design terminology) and their levels.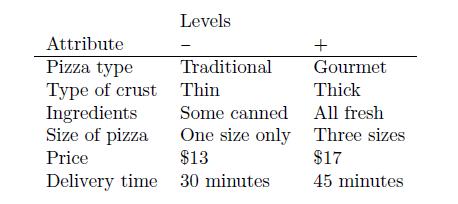

The alternatives that customers must choose from in a survey are all 26 combinations of attribute levels.

(a) Since it would be impractical to ask a potential customer to choose from a list of 26 = 64 combinations, it would be better to have each customer surveyed make a choice from four alternatives. Create a blocked 26 design with block size four, so that each customer surveyed must only choose from among the four combinations of attribute levels in one block.

(b) Since higher-order interactions are unlikely to be important, construct a 16-run 26−2 design blocked into four blocks of size four. Are all main eects estimable from your design?

(c) Block a 16-run 26−2 design blocked into eight blocks of size two, so that each customer surveyed only has to choose between two alternatives. Are all main eects estimable from this design?

(d) If the number of alternatives of the type of crust and the size of pizza were increased from 2 to 3, the factorial combination of all attribute levels would change from a 26 to a 24 × 32 factorial. Using the optBlock function in AlgDesign, create a 24-run fraction of a 24 × 32 factorial, blocked in 8 blocks of 3, for this problem.

(e) What model would you use for the analysis of data arising from the design you created in (d)?

Levels Attribute Pizza type Type of crust Ingredients Traditional Thin Some canned Size of pizza Price One size only $13 Delivery time 30 minutes + Gourmet Thick All fresh Three sizes $17 45 minutes