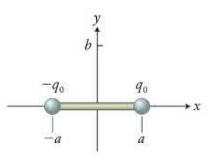
A short wire runs along an \(x\) axis from \(x=a\) to \(x=-a\) (Figure P30.30). At \(t=0\), there is a small sphere carrying charge \(+q_{0}\) at \(x=a\) and a small sphere carrying charge \(-q_{0}\) at \(x=-a\). As the spheres discharge and a current is established in the wire, show that, for \(t>0\), the generalized form of Ampère's law (Eq. 30. 13) and the Biot-Savart law (Eq. 28. 12) give the same result for the magnitude of the magnetic field a distance \(b\) up the \(y\) axis. (Hint: Obtain the electric flux through a circular disk in the \(y z\) plane, centered at the origin. Because the electric field is not constant over the surface of the disk, you must divide the disk into a nested set of rings of various radii and integrate. A representative ring should have radius \(r\) and radial extent \(d r\).)

Data from Figure P30.30

Data from Eq. 28. 12

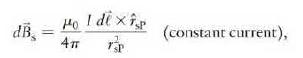
Data from Eq. 28. 13

-90 a b 90 x+