For a system of two identical cars, (A) and (B), of the same inertia (m) but moving

Question:

For a system of two identical cars, $A$ and $B$, of the same inertia $m$ but moving at two different velocities, $v_{\Lambda}$ and $v_{\mathrm{B}}$, show that the kinetic energy of the two-car system can be expressed as the sum of two terms: the kinetic energy of a double car moving with one-half the sum of their velocities, plus the kinctic energy of a double car moving with one-half the difference of their velocities:

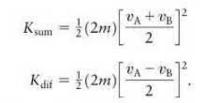
image text in transcribed