For the system described in Problem 71, you measure a constant speed of \(1.0 \mathrm{~m} / \mathrm{s}\). Because this is not the value you calculated when you ignored friction in the system, you conclude that the friction in the rails is too great to be ignored. What value for the coefficient of kinetic friction \(\mu_{k}\) yields the \(1.0-\mathrm{m} / \mathrm{s}\) speed you measured?

Data from Problem 71

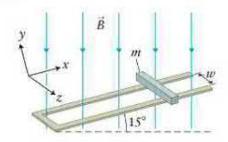
A conducting bar of width \(w=0.12 \mathrm{~m}\) and mass \(m=\) \(8.0 \mathrm{~g}\) can slide freely on two parallel conducting rails positioned at an incline of \(\theta=15^{\circ}\) (Figure P29.71). The rails are connected at their base by a piece of conducting material. The distance between the rails is \(w\), and the resistance in the rails is \(R=0.20 \mathrm{~V} / \mathrm{A}\). A uniform magnetic field \(\vec{B}\) is exactly vertical as indicated in the drawing, with \(B=0.50 \mathrm{~T}\). At what constant (terminal) speed does the bar slide down the incline? Ignore friction.

Data from Figure P29.71

Transcribed Image Text:

100 B m W 1.5