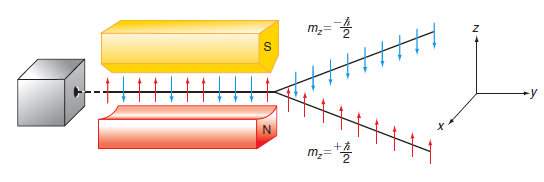
In this problem, you will carry out the calculations that describe the Stern€“Gerlach experiment shown in Figure 17.2. Classically, a magnetic dipole μ has the potential energy E = ˆ’μ €¢ B. If the field has a gradient in the z direction, the magnetic moment will experience a force, leading it to be deflected in the z direction. Because classically μ can take on any value in the range ˆ’ ˆ£Î¼ˆ£ ‰¤ μ_z‰¤ ˆ£Î¼ˆ£, a continuous range of positive and negative z deflections of a beam along the y direction will be observed. From a quantum mechanical perspective, the forces are the same as in the classical picture, but μ z can only take on a discrete set of values. Therefore, the incident beam will be split into a discrete set of beams that have different deflections in the z direction. 

a. The geometry of the experiment is shown here. In the region of the magnet indicated by d₁, the Ag atom experiences a constant force. It continues its motion in the force-free region indicated by d₂.

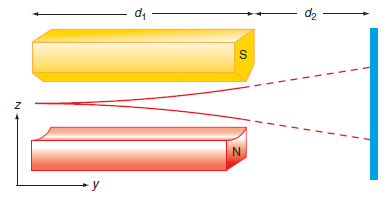
If the force inside the magnet is F_z, show that ˆ£zˆ£ = 1/2(F_z/m _Ag)t²₁ + t₂v_z (t₁). The times t₁ and t₂ correspond to the regions d₁ and d₂.

b. Show that, assuming a small deflection,

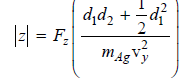
c. The magnetic moment of the electron is given by ˆ£Î¼ˆ£ = g_Sμ_B/2. In this equation, μ_B is the Bohr magneton and has the value 9.274 × 10^€“24 J/T. The gyromagnetic ratio of the electron g_S has the value 2.00231. If ˆ‚B_z/ˆ‚z = 750. T m^€“1, and d₁ and d₂ are 0.175 and 0.225 m, respectively, and v _y = 475 m s^€“1, what values of z will be observed?

Figure 17.2

Transcribed Image Text:

d, -y dịd, + -d? 2 |z| = F. .2 тAg У 4g'y