In this problem, you will solve for the total energy eigenfunctions and eigenvalues for an electron in a finite depth box. We first go through the calculation for the box parameters used in Figure 16.1. You will then carry out the calculation for a different set of parameters. We describe the potential in this way:

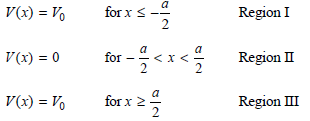
The eigenfunctions must have the following form in these three regions:

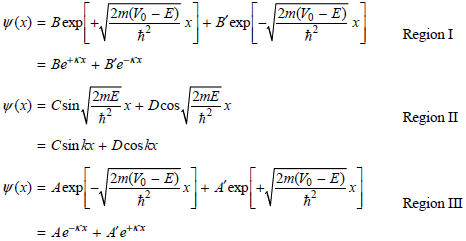
So that the wave functions remain finite at large positive and negative values of x, A′ = B′ = 0. An additional condition must also be satisfied. To arrive at physically meaningful solutions for the eigenfunctions, the wave functions in the separate regions must have the same amplitude and derivatives at the values of x = a/2 and

x = −a/2 bounding the regions. This restricts the possible values for the coefficients A, B, C, and D. Show that applying these conditions gives the following equations:

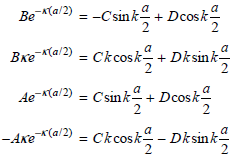
These two pairs of equations differ on the right side only by the sign of one term. We can obtain a set of equations that contain fewer coefficients by adding and subtracting each pair of equations to give

Transcribed Image Text:

V(x) = Vo for x - N/A 2 V(x) = 0 for V(x) = Vo for x 02 Region I Region II Region III