The following two reactions take place in a gas-phase reactor: If the system comes to equilibrium at
Question:
The following two reactions take place in a gas-phase reactor:
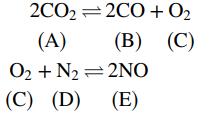
If the system comes to equilibrium at 3000 K and 1 atm, the product gas mole fractions satisfy the relations
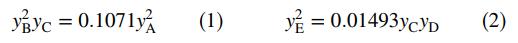
(a) Let nA0; ... ; nE0 be the initial number of gram-moles of each species and ξe1 and ξe2 be the extents of reactions 1 and 2, respectively, at equilibrium (see Equation 4.6-7). Derive expressions for the mole fractions yA; yB ; ... ; yE in terms of nA0; nB0; ... ; nE0, ξe1, and ξe2. Then substitute in the equilibrium relations to derive two simultaneous equations for the two extents of reaction.
(b) One-third of a gram-mole each of CO2, O2, and N2 are charged into a batch reactor and the reactor contents equilibrate at 3000 K and 1 atm. Without doing any calculations, prove that you have enough information to calculate the component mole fractions of the reactor contents at equilibrium.
(c) Create a spreadsheet and input the sets of values of nA0, nB0, nC0, nD0, and nE0 shown below, and two initial guesses for ξ1 and ξ2 (make them each 0.1). Then for each set, have the spreadsheet calculate nA, nB, nC, nD, nE from Eq. (4.6-7); then ntotal and yA, yB, yC, yD, and yE; and then the squares of the left-hand side minus the right-hand side of Equations (1) and (2). Finally, use Solver to find the values of ξ1 and ξ2 that minimize the sum of those two squares. When you call Solver the
Equation 4.6-7
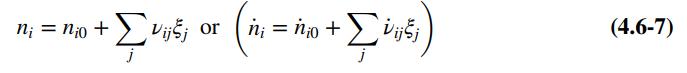
Step by Step Answer:

Elementary Principles of Chemical Processes
ISBN: 978-1119498759
4th edition
Authors: Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard





