Alpha decay occurs when an alpha particle tunnels through the Coulomb barrier. FIGURE CP42.63 shows a simple one-dimensional model of the potential-energy well of an alpha particle in a nucleus with A ≈ 235. The 15 fm width of this one-dimensional potential-energy well is the diameter of the nucleus. Further, to keep the model simple, the Coulomb barrier has been modeled as a 20-fm wide, 30-MeV-high rectangular potential-energy barrier. The goal of this problem is to calculate the half-life of an alpha particle in the energy level E = 5.0 Me V.

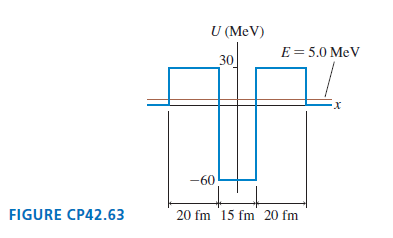
a. What is the kinetic energy of the alpha particle while inside the nucleus? What is its kinetic energy after it escapes from the nucleus?
b. Consider the alpha particle within the nucleus to be a point particle bouncing back and forth with the kinetic energy you found in part a. What is the particle’s collision rate, the number of times per second it collides with a wall of the potential?
c. What is the tunneling probability P_tunnel?
d. P_tunnel is the probability that on any one collision with a wall the alpha particle tunnels through instead of reflecting. The probability of not tunneling is 1 - P_tunnel. Hence the probability that the alpha particle is still inside the nucleus after N collisions is (1 - P_tunnel )^N ≈ 1 - N_Ptunnel, where we’ve used the binomial approximation because P_tunnel