In calculus you will learn that, if is a polynomial function, then the derivative of P(x) is
Question:
In calculus you will learn that, if
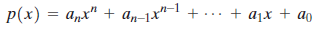
is a polynomial function, then the derivative of P(x) is
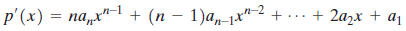
Newton's Method is an efficient method for approximating the x-intercepts (or real zeros) of a function, such as p(x). The following steps outline Newton's Method.
STEP 1: Select an initial value that is somewhat close to the x-intercept being sought.
STEP 2: Find values for x using the relation
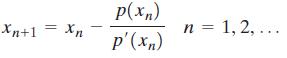
until you get two consecutive values xn and xn+1 that agree to whatever decimal place accuracy you desire.
STEP 3: The approximate zero will be xn+1.
Consider the polynomial p(x) = x3 - 7x - 40.
(a) Evaluate p(5) and p(-3).
(b) What might we conclude about a zero of p? Explain.
(c) Use Newton's Method to approximate an x-intercept, r, -3 < r < 5, of p(x) to four decimal places.
(d) Use a graphing utility to graph p(x) and verify your answer in part (c).
(e) Using a graphing utility, evaluate p(r) to verify your result.
Step by Step Answer:






