Problems 89 and 90 require the following discussion: The shortest distance between two points on Earth’s surface can be determined from the latitude and longitude of the two locations. For example, if location 1 has (lat, lon) = (α₁, β₁) and location 2 has (lat, lon) = (α₂, β₂), the shortest distance between the two locations is approximately d = r cos⁻¹ [(cosα₁ cosβ₁ cosα₂ cosβ₂) + (cosα₁ sinβ₁ cosα₂ sinβ₂) + (sinα₁ sinα₂)]. where r = radius of Earth ≈ 3960 miles and the inverse cosine function is expressed in radians. Also, N latitude and E longitude are positive angles, and S latitude and W longitude are negative angles.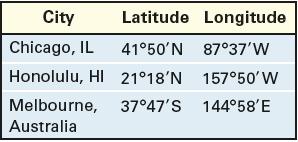

Find the shortest distance from Chicago, latitude 41°50' N, longitude 87°37' W, to Honolulu, latitude 21°18' N, longitude 157°50' W. Round your answer to the nearest mile.

City Latitude Longitude Chicago, IL 4150N 8737'W Honolulu, HI 2118'N 15750' W 14458'E Melbourne, 3747'S Australia