When a smaller pipe branches off from a larger one in a flow system, we may want it to run off at an angle that is best from some energysaving point of view. We might require, for instance, that energy loss due to friction be minimized along the section AOB shown in the accompanying figure. In this diagram, B is a given point to be reached by the smaller pipe, A is a point in the larger pipe upstream from B, and O is the point where the branching occurs. A law due to Poiseuille states that the loss of energy due to friction in nonturbulent flow is proportional to the length of the path and inversely proportional to the fourth power of the radius. Thus, the loss along AO is (kd₁)/R⁴ and along OB is (kd₂)/r⁴, where k is a constant, d₁ is the length of AO, d₂ is the length of OB, R is the radius of the larger pipe, and r is the radius of the smaller pipe. The angle θ is to be chosen to minimize the sum of these two losses: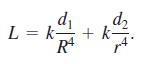

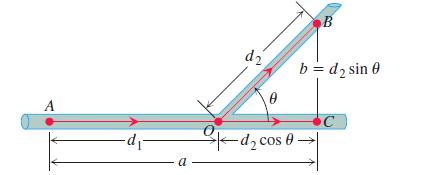
In our model, we assume that AC = a and BC = b are fixed. Thus we have the relations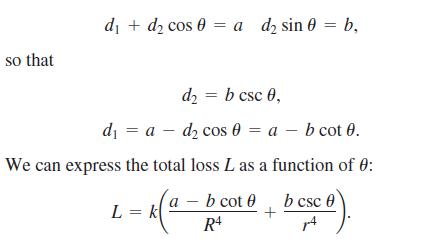

a. Show that the critical value of θ for which dL/dθ equals zero is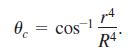

b. If the ratio of the pipe radii is r/>R = 5/6, estimate to the nearest degree the optimal branching angle given in part (a).

Transcribed Image Text:

d₁ d₂ +k- -Y = 7 Rª it