Consider a signal plus noise process of the form z(t) A cos 2 (f 0 f d )t n(t) (D 29) where n(t) is given by n(t) n c (t) cos 2 f 0 t n s (t) sin 2 f 0 t (D 30) Assume that n(t) is an ideal band limited white noise process with double sided power spectral density equal to 1 2 N 0 , for 1 2 B f f 0 ...

a The expression for nct and ns ...

Consider a signal-plus-noise process of the form z(t) = A cos 2?(f 0 + f d )t

Question:

Consider a signal-plus-noise process of the form

z(t) = A cos 2?(f₀ + f_d)t + n(t)? ? ? ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ??(D.29)

where n(t) is given by

n(t) = n_c(t) cos 2?f₀t ? n_s(t) sin 2?f₀t? ? ? ? ? ? ? ? ? ? ? ? ?(D.30)

Assume that n(t) is an ideal band limited white-noise process with double-sided power spectral density equal to 1/2 N₀, for -1/2 B ? f ? f₀ ? 1/2 B, and zero otherwise. Write z(t) as

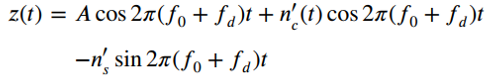
(a) Express n?_c(1) and n?_s (t) in terms of n_c(t) and n_s (t). Find the power spectral densities of n?_c(t) and n?_s(t), S?_nc(f) and S_n?s(f).?

(b) Find the cross-spectral density of n?_c(t) and n?_s(t), S_n?cn?s (f), and the cross-correlation function, R_n?cn?s (?). Are n?_c(t) and n?_s(t) correlated? Are n?_c(t) and n?_s(t), sampled at the same instant, independent?