Consider a transform-limited pulse of center frequency f = 10 GHz, and of full-width 2T = 1.0
Question:
In Problem
Show that the group dispersion parameter, d2β/dω2, for a given mode in a parallel-plate or rectangular waveguide is given by

where ωc is the radian cutoff frequency for the mode in question [note that the first derivative form was already found, resulting in Eq. (57)].
Eq. (57)
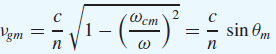
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





